Lecture 23: Bayesian Adaptive Regression Kernels

STA702

Merlise Clyde

Duke University

Nonparametric Regression

  • Consider model \(Y_1, \dots, Y_n \sim \textsf{N}\left(\mu(\mathbf{x}_i), \sigma \right)\)

  • Mean function represented via a Stochastic Expansion \[\mu(\mathbf{x}_i) = \sum_{j \le J} b_j(\mathbf{x}_i, \boldsymbol{\omega}_j) \beta_j\]

  • Multivariate Gaussian Kernel \(g\) with parameters \(\boldsymbol{\omega}= (\boldsymbol{\chi}, \boldsymbol{\Lambda})\) \[ b_j(\mathbf{x}, \boldsymbol{\omega}_j) = g( \boldsymbol{\Lambda}_j^{1/2} (\mathbf{x}- \boldsymbol{\chi}_j)) = \exp\left\{-\frac{1}{2}(\mathbf{x}- \boldsymbol{\chi}_j)^T \boldsymbol{\Lambda}_j (\mathbf{x}- \boldsymbol{\chi}_j)\right\} \]

  • introduce a Lévy measure \(\nu( d\beta, d \boldsymbol{\omega})\)

  • Poisson distribution \(J \sim \textsf{Poi}(\nu_+)\) where \(\nu_+\equiv \nu(\mathbb{R}\times\boldsymbol{\Omega}) = \iint \nu(\beta, \boldsymbol{\omega}) d \beta \, d\boldsymbol{\omega}\) \[\beta_j,\boldsymbol{\omega}_j \mid J \mathrel{\mathop{\sim}\limits^{\rm iid}}\pi(\beta, \boldsymbol{\omega}) \propto \nu(\beta,\boldsymbol{\omega})\]

Function Spaces

  • Conditions on \(\nu\)

    • need to have that \(|\beta_j|\) are absolutely summable
    • finite number of large coefficients (in absolute value)
    • allows an infinite number of small \(\beta_j \in [-\epsilon, \epsilon]\)

  • satisfied if \[\iint_{\mathbb{R}\times \boldsymbol{\Omega}}( 1 \wedge |\beta|) \nu(\beta, \boldsymbol{\omega}) d\beta \, d\boldsymbol{\omega}< \infty\]

  • Mean function \(\textsf{E}[Y_i \mid \boldsymbol{\theta}] = \mu(\mathbf{x}_i, \boldsymbol{\theta})\) falls in some class of nonlinear functions based on \(g\) and prior on \(\boldsymbol{\Lambda}\)

    • Besov Space
    • Sobolov Space

Inference via Reversible Jump MCMC

  • number of support points \(J\) varies from iteration to iteration

    • add a new point (birth)
    • delete an existing point (death)
    • combine two points (merge)
    • split a point into two

  • update existing point(s)

  • can be much faster than shrinkage or BMA with a fixed but large \(J\)

So far

  • more parsimonious than “shrinkage” priors or SVM with fixed \(J\)

  • allows for increasing number of support points as \(n\) increases (adapts to smoothness)

  • no problem with non-normal data, non-negative functions or even discontinuous functions

  • credible and prediction intervals; uncertainty quantification

  • robust alternative to Gaussian Process Priors

  • But - hard to scale up random scales & locations as dimension of \(\mathbf{x}\) increases

  • Alternative Prior Approximation II

Higher Dimensional \(\mathbf{X}\)

MCMC is (currently) too slow in higher dimensional space to allow

  • \(\boldsymbol{\chi}\) to be completely arbitrary; restrict support to observed \(\{\mathbf{x}_i\}\) like in SVM (or observed quantiles)

  • use a common diagonal \(\boldsymbol{\Lambda}\) for all kernels

  • Kernels take form: \[\begin{aligned} b_j(\mathbf{x}, \boldsymbol{\omega}_j) & = & \prod_d \exp\{ -\frac{1}{2} \lambda_d (x_d - \chi_{dj})^2 \} \\ \mu(\mathbf{x}) & = & \sum_j b_j(\mathbf{x}, \boldsymbol{\omega}_j) \beta_j \end{aligned}\]

  • accomodates nonlinear interactions among variables

  • ensemble model like random forests, boosting, BART, SVM

Approximate Lévy Prior II

  • \(\alpha\)-Stable process: \(\nu(d\beta, d \boldsymbol{\omega}) = \gamma c_\alpha |\beta|^{-(\alpha + 1)} d\beta \ \pi(d \boldsymbol{\omega})\)

  • Continuous Approximation to an \(\alpha\)-Stable process via a Student \(t(\alpha, 0, \epsilon)\): \[\nu_\epsilon(d\beta, d \boldsymbol{\omega}) = \gamma c_\alpha (\beta^2 + \alpha \epsilon^2)^{-(\alpha + 1)/2} d\beta \ \pi(d \boldsymbol{\omega})\]

  • Based on the following hierarchical prior

    _j _j & N(0, _j^-1) & & _j Gamma(, )
    J & ~Poi(^+_) & & ^+_= _(, ) = ()

Key Idea: need to have variance/scale of coefficients decrease as \(J\) increases

Limiting Case

\[\begin{aligned} \beta_j \mid \varphi_j & \mathrel{\mathop{\sim}\limits^{\rm ind}}&\textsf{N}(0, 1/\varphi_j) \\ \varphi_j & \mathrel{\mathop{\sim}\limits^{\rm iid}}& \textsf{Gamma}(\alpha/2, 0) \end{aligned}\]

Notes:

  • Require \(0 < \alpha < 2\) Additional restrictions on \(\omega\)

  • Tipping’s Relevance Vector Machine corresponds to \(\alpha = 0\) (improper posterior!)

  • Provides an extension of Generalized Ridge Priors to infinite dimensional case

  • Cauchy process corresponds to \(\alpha = 1\)

  • Infinite dimensional analog of Cauchy priors

Simplification with \(\alpha = 1\)

  • Poisson number of points \(J \sim \textsf{Poi}(\gamma/\boldsymbol{\epsilon})\)

  • Given \(J\), \([ n_1 : n_n] \sim \textsf{MultNom}(J, 1/(n+1))\) points supported at each kernel located at \(\mathbf{x}_j\)

  • Aggregating, the regression mean function can be rewritten as \[\mu(\mathbf{x}) = \sum_{i=0}^n \tilde{\beta}_i b_j(\mathbf{x}, \boldsymbol{\omega}_i), \quad \tilde{\beta}_i = \sum_{\{j \, \mid \boldsymbol{\chi}_j = \mathbf{x}_i\}} \beta_j\]

if \(\alpha = 1\), not only is the Cauchy process infinitely divisible, the approximated Cauchy prior distributions for \(\beta_j\) are also infinitely divisible!

\[ \tilde{\beta}_i \mathrel{\mathop{\sim}\limits^{\rm ind}} \textsf{N}(0, n_i^2 \tilde{\varphi}_i^{-1}), \qquad \tilde{\varphi}_i \mathrel{\mathop{\sim}\limits^{\rm iid}}\textsf{Gamma}( 1/2, \boldsymbol{\epsilon}^2/2) \]

At most \(n\) non-zero coefficients!

Inference for Normal Model

  • integrate out \(\tilde{\boldsymbol{\beta}}\) for marginal likelihood \(\cal{L}(J, \{n_i\}, \{\tilde{\varphi}_i\}, \sigma^2, \boldsymbol{\lambda})\) \[\mathbf{Y}\mid \sigma^2, \{n_i\}, \{\tilde{\varphi}_i\}, \boldsymbol{\lambda}\sim \textsf{N}\left(\mathbf{0}_n, \sigma^2 \mathbf{I}_n + \mathbf{b} \, \textsf{diag}\left(\frac{n_i^2}{\tilde{\varphi}_i} \right)\mathbf{b}^T\right)\]

  • if \(n_i = 0\) then the kernel located at \(\mathbf{x}_i\) drops out so we still need birth/death steps via RJ-MCMC for \(\{n_i, \tilde{\varphi}_i\}\)

  • for \(J < n\) take advantage of the Woodbury matrix identity for matrix inversion likelihood \[(A + U C V)^{-1} = A^{-1} - A^{-1}U(C^{-1} + VA^{-1}U){-1} V A^{-1}\]

  • update \(\sigma^2, \boldsymbol{\lambda}\) via usual MCMC

  • for fixed \(J\) and \(\{n_i\}\), can update \(\{\tilde{\varphi}_i\}, \sigma^2, \boldsymbol{\lambda})\) via usual MCMC (fixed dimension)

Feature Selection in Kernel

  • Product structure allows interactions between variables
  • Many input variables may be irrelevant
  • Feature selection; if \(\lambda_d = 0\) variable \(\mathbf{x}_d\) is removed from all kernels
  • Allow point mass on \(\lambda_d = 0\) with probability \(p_\lambda \sim \textsf{Beta}(a,b)\) (in practice have used \(a = b = 1\)
  • can also constrain all \(\lambda_d\) that are non-zero to be equal across dimensions

Binary Regression

  • add latent Gaussian variable as in Albert & Chib

bark package

library(bark)
set.seed(42)
n = 500
circle2 = data.frame(sim_circle(n, dim = 2))
plot(x.1 ~ x.2, data=circle2, col=y+1)

Circle Data Classification

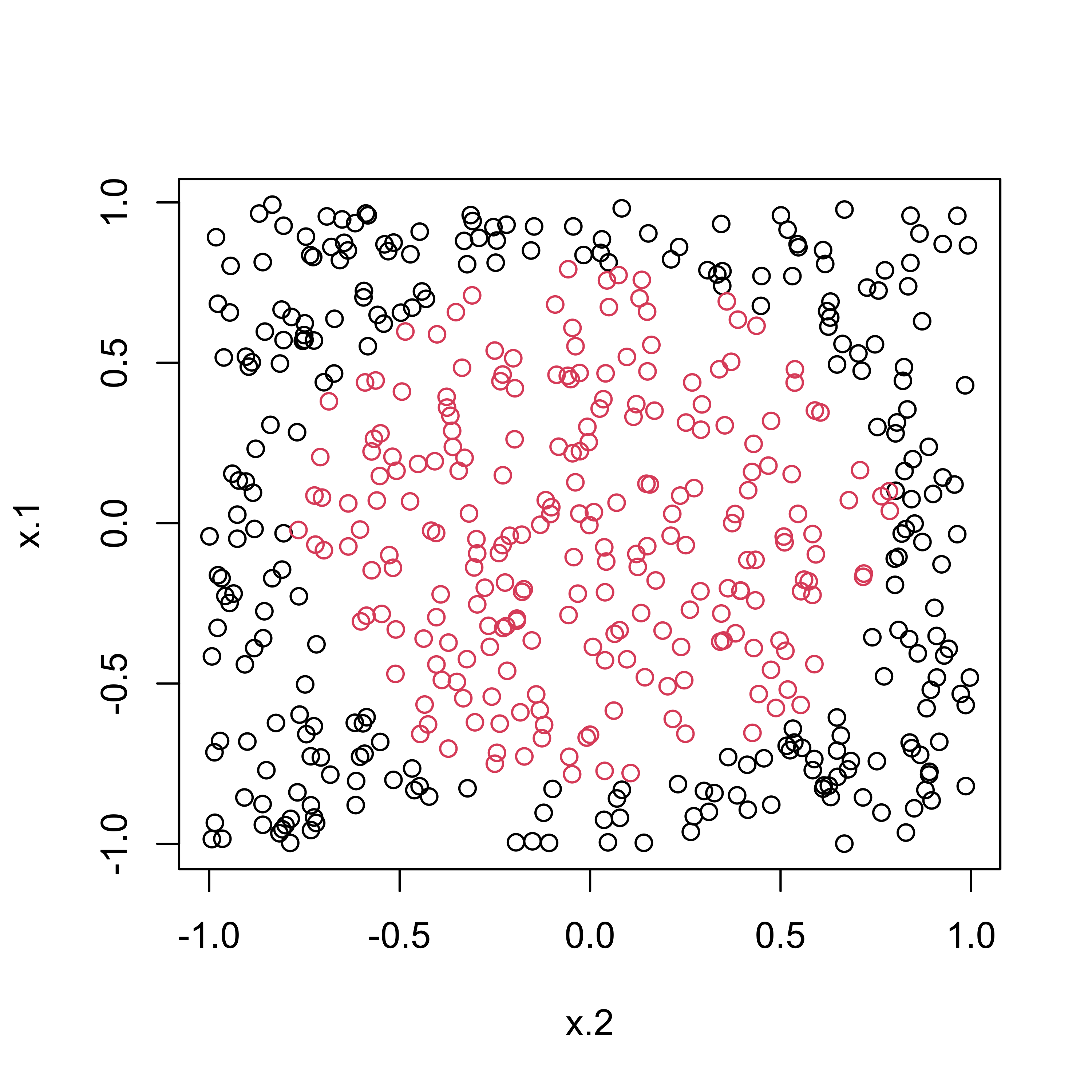
BARK Classification

set.seed(42)
train = sample(1:n, size = floor(n/2), rep=FALSE)
circle2.bark = bark(y ~ . , data = circle2,
                    subset = train,
                    testdata = circle2[-train,],
                    classification = TRUE,
                    printevery = 10000,
                    selection = TRUE, 
                    common_lambdas = TRUE)

  • classification = TRUE for probit regression

  • selection = TRUE allows some of the \(\lambda_j\) to be 0

  • common_lambdas = TRUE sets all (non-zero) \(\lambda_j\) to a common \(\lambda\)

Missclassification

misscl = (circle2.bark$yhat.test.mean > 0) != circle2[-train, "y"]
plot(x.1 ~ x.2, data=circle2[-train,], pch=circle2[-train, "y"]+1, col=misscl + 1)
title(paste("Missclassification Rate", round(mean(misscl), 4)))

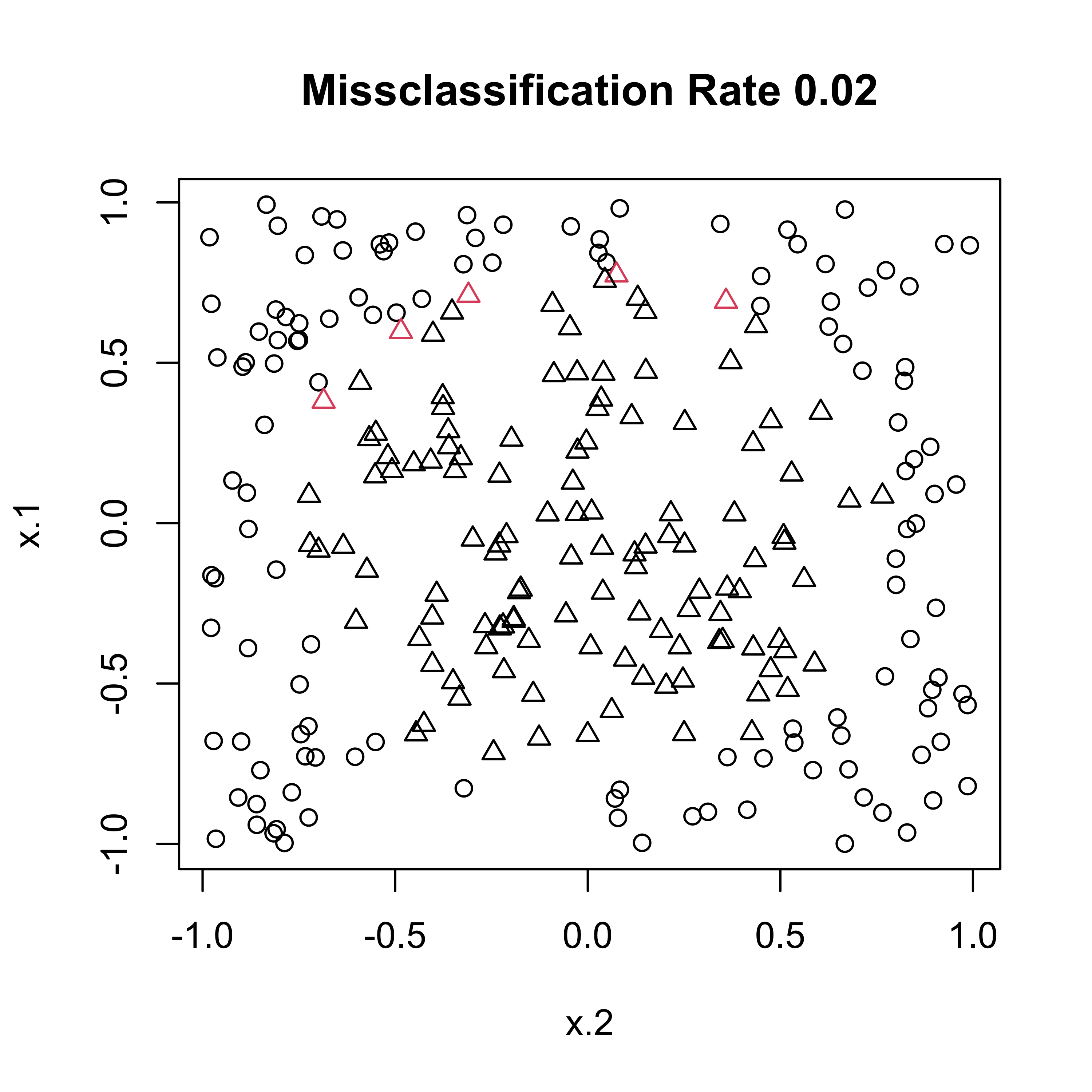
Support Vector Machines (SVM) & BART

library(e1071)
circle2.svm = svm(y ~ x.1 + x.2, data=circle2[train,],
                  type="C")
pred.svm = predict(circle2.svm, circle2[-train,])
mean(pred.svm != circle2[-train, "y"])
[1] 0.048
suppressMessages(library(BART))
circle.bart = pbart(x.train = circle2[train, 1:2],
                    y.train = circle2[train, "y"])
pred.bart = predict(circle.bart, circle2[-train, 1:2])
misscl.bart = mean((pred.bart$prob.test.mean > .5) != 
              circle2[-train, "y"])
[1] 0.036

Comparisons

Data Sets n p BARK-D BARK-SE BARK-SD SVM BART
Circle 2 200 2 4.91% 1.88% 1.93% 5.03% 3.97%
Circle 5 200 5 4.70% 1.47% 1.65% 10.99% 6.51%
Circle 20 200 20 4.84% 2.09% 3.69% 44.10% 15.10%
Bank 200 6 1.25% 0.55% 0.88% 1.12% 0.50%
BC 569 30 4.02% 2.49% 6.09% 2.70% 3.36%
Ionosphere 351 33 8.59% 5.78% 10.87% 5.17% 7.34%
  • BARK-D: different \(\lambda_d\) for each dimension
  • BARK-SE: selection and equal \(\lambda_d\) for non-zero \(\lambda_d\)
  • BARK-SD: selection and different \(\lambda_d\) for non-zero \(\lambda_d\)

Needs & Limitations

  • NP Bayes of many flavors often does better than frequentist methods (BARK, BART, Treed GP, more)
  • Hyper-parameter specification - theory & computational approximation
  • asymptotic theory (rates of convergence)
  • need faster code for BARK that is easier for users (BART & TGP are great!)
  • Can these models be added to JAGS, STAN, etc instead of stand-alone R packages
  • With availability of code what are caveats for users?

Summary

Lévy Random Field Priors & LARK/BARK models:

  • Provide limit of finite dimensional priors (GRP & SVSS) to infinite dimensional setting
  • Adaptive bandwidth for kernel regression
  • Allow flexible generating functions
  • Provide sparser representations compared to SVM & RVM, with coherent Bayesian interpretation
  • Incorporation of prior knowledge if available
  • Relax assumptions of equally spaced data and Gaussian likelihood
  • Hierarchical Extensions
  • Formulation allows one to define stochastic processes on arbitrary spaces (spheres, manifolds)

https://sta702-F23.github.io/website/