Lecture 21: Hamiltonian Monte Carlo

STA702

Merlise Clyde

Duke University

Gibbs sampling

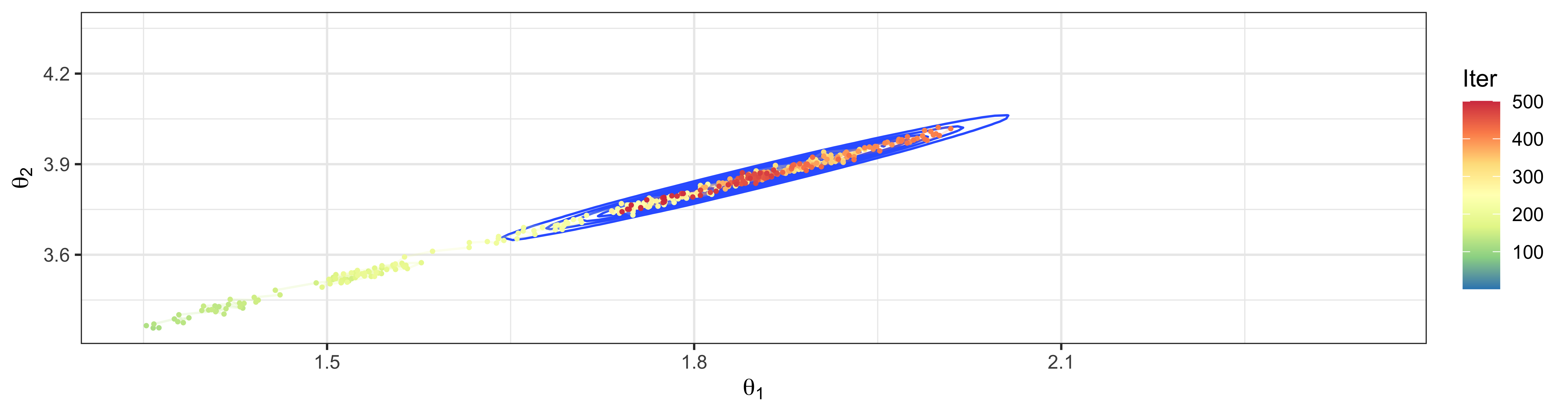
Consider model \[ \begin{aligned} \boldsymbol{Y}_1, \dots, \boldsymbol{Y}_n &\sim \textsf{N}_2 \left(\boldsymbol{\theta}, \boldsymbol{\Sigma}\right); \\ \theta_j &\sim \textsf{N}(0, 1)~~~~~~j=1,2. \end{aligned} \]
Suppose that the covariance matrix \(\boldsymbol{\Sigma}\) is known and has the form \[\boldsymbol{\Sigma}= \left[\begin{array}{cc} 1 & \rho \\ \rho & 1 \end{array}\right]\]
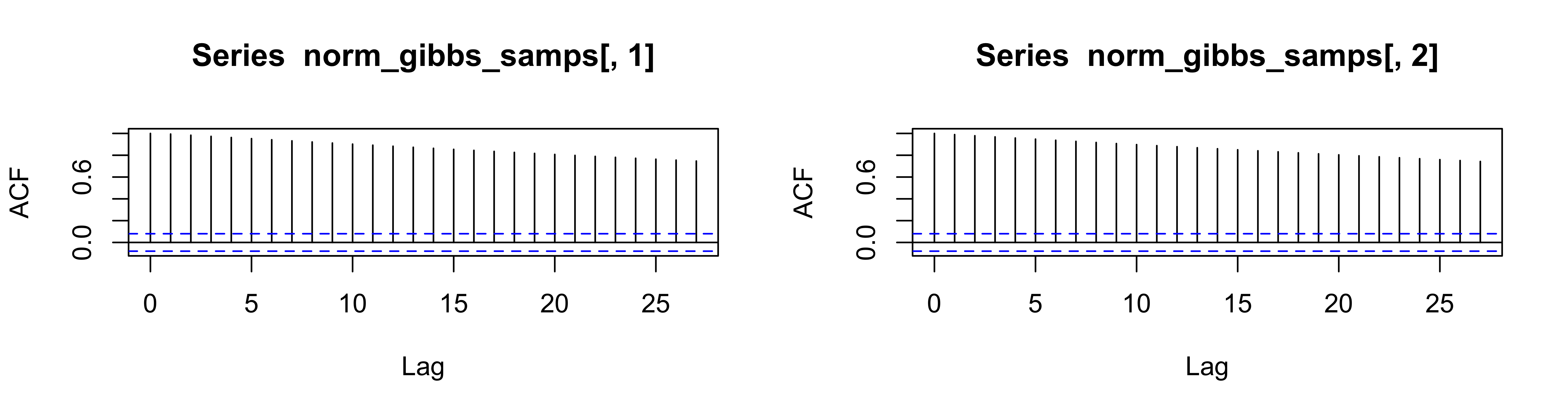
What happens when \(\rho = 0.995\) for sampling from full conditionsals for \(\theta_1\) and \(\theta_2\)?

Gibbs vs Stan samples

ACF

Hamiltonian Monte Carlo (HMC)

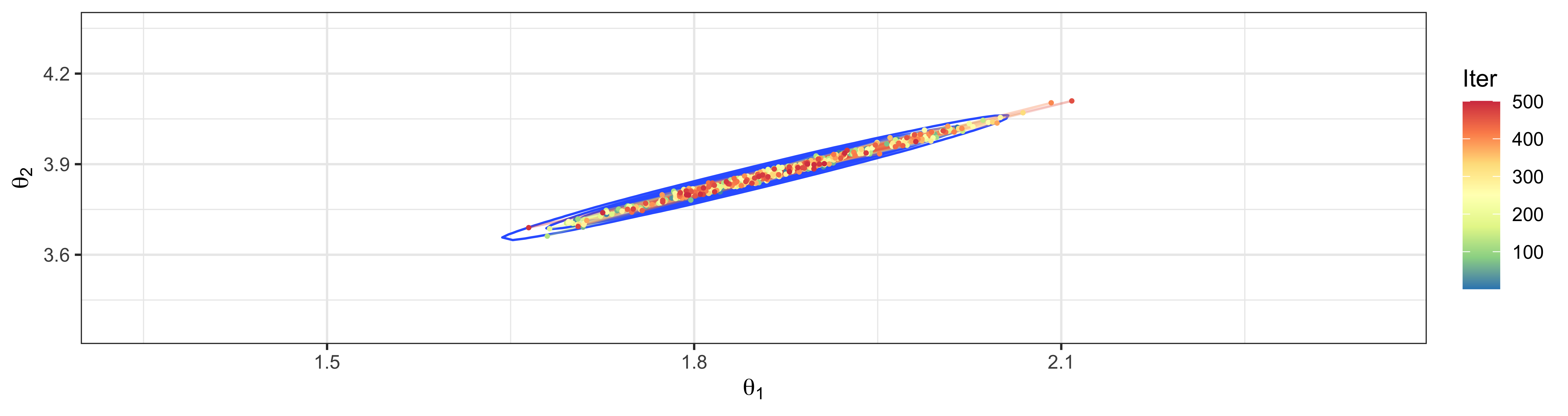
HMC creates transitions that efficiently explore the parameter space by using concepts from Hamiltonian mechanics.
In Hamiltonian mechanics, a physical system is specified by positions \(\mathbf{q}\) and momenta \(\mathbf{p}\).
A space defined by these coordinates is called a phase space
If the parameters of interest in a typical MCMC method are denoted as \(q_1, \dots, q_K\), then HMC introduces auxiliary momentum parameters \(p_1, \dots, p_K\) such that the algorithm produces draws from the joint density: \[ \pi( \mathbf{q}, \mathbf{p}) = \pi (\mathbf{p} | \mathbf{q}) \pi(\mathbf{q}) \]
marginalizing over the \(p_k\)’s, we recover the marginal distribution of the \(q_k\)’s Therefore, if we create a Markov Chain that converges to \(\pi(\mathbf{q}, \mathbf{p})\), we have immediate access to samples from \(\pi(\mathbf{q})\), which is our target distribution.

Hamiltonian

Hamilton’s equations describe the time evolution of the system in terms of the Hamiltonian, \(\mathcal{H}\), which corresponds to the total energy of the system: \[\mathcal{H}(\mathbf{p},\mathbf{q}) = K(\mathbf{q}, \mathbf{p}) + U(\mathbf{q})\]
\(K(\mathbf{q}, \mathbf{p})\) represents the kinetic energy of the system and is equal to the negative logarithm of the momentum distribution, e.g. \[K(\mathbf{p}) = \frac{\mathbf{p}^T \mathbf{M}^{-1} \mathbf{p}}{2} = \sum_ i \frac{p_i^2}{2 m_i}\]
\(\mathbf{M}\) is the Mass matrix
\(U(\mathbf{q})\) the potential energy of the system; equal to the negative logarithm of the distribution of \(\mathbf{q}\).
Joint \(\pi(\mathbf{q}, \mathbf{p}) \propto e^{- \cal{H}(\mathbf{q}, \mathbf{p})} = e^{- K(\mathbf{p})} e^{- U(\mathbf{q})}\)

Evolution

At each iteration of the sampling algorithm, HMC implementations make draws from some distribution \(\pi(\mathbf{p} | \mathbf{q})\) and then evolves the system \((\mathbf{q}, \mathbf{p})\) to obtain the next sample of \(\mathbf{q}\).
To “evolve the system” is to move \((\mathbf{q}, \mathbf{p})\) forward in “time,” i.e. to change the values of \((\mathbf{q}, \mathbf{p})\) according to Hamilton’s differential equations: \[\begin{align} \frac{d \mathbf{p}}{dt} &= - \frac{\partial \mathcal{H}}{\partial \mathbf{q}} = -\frac{\partial K}{\partial \mathbf{q}} - \frac{\partial U}{\partial \mathbf{q}} \\ \frac{d \mathbf{q}}{dt} &= +\frac{\partial \mathcal{H}}{\partial \mathbf{p}} = +\frac{\partial K}{\partial \mathbf{p}} \end{align}\]
Defines a mapping \(T_s\) from the state at any time \(t\) to the state at \(t+s\)

“The differential change in momentum parameters \(\mathbf{p}\) over time is governed in part by the differential information of the density over the target parameters.”

Key Properties

Reversibility The mapping of the state at time \(t\) \((\mathbf{p}(t), \mathbf{q}(t))\) to the state at \(t+s\) \((\mathbf{p}(t+s), \mathbf{q}(t+s))\) is one-to-one and we have an inverse \(T_{-s}\) - obtained by negating the derivatives; \(K(\mathbf{p}) = K(-\mathbf{p})\) MCMC updates using the dymamics don’t modify invariant distribution!
Invariance/Conservation the dymamics keep the Hamiltonian invariant - if we use the dynamics to generate proposals, the acceptance probability of MH is equal to one if \(\cal{H}\) is kept invariant!
Volume Preservation/Symplectiness the mapping \(T_s\) of a region \(R\) to \(T_s(R)\) preserves volume means that we do not need to compute Jacobians

in practice we need to use approximations to solve the PDE’s so won’t have exact invariance etc so acceptance probability is not 1!

Approximate Solutions to Differential Eqs

Discretize time into steps \(\epsilon\)
Euler’s Method for \(i\)th coordinate \[\begin{align} p_i(t + \epsilon) & = p_i(t) + \epsilon \frac{d p_i}{t}(t) = p_i(t) - \epsilon \frac{\partial U(q_i(t))} {\partial q_i} \\ q_i(t + \epsilon) & = q_i(t) + \epsilon \frac{d q_i}{t}(t) = q_i(t) + \epsilon \frac{\partial K(p_i(t))} {\partial p_i} = q_i(t) + \epsilon \frac{p_i(t)}{m_i}\\ \end{align}\]
Modified Euler method \[\begin{align} p_i(t + \epsilon) & = p_i(t) - \epsilon \frac{\partial U(q_i(t))} {\partial q_i} \\ q_i(t + \epsilon) & = q_i(t) + \epsilon \frac{p_i(t + \epsilon)}{m_i}\\ \end{align}\]

Leapfrog

Divide into half steps
apply Modified Euler \[\begin{align} p_i(t + \epsilon/2) & = p_i(t) - \frac{\epsilon}{2} \frac{\partial U(q_i(t))} {\partial q_i} \\ q_i(t + \epsilon) & = q_i(t) + \epsilon \frac{p_i(t + \epsilon/2)}{m_i}\\ p_i(t + \epsilon) & = p_i(t) - \frac{\epsilon}{2} \frac{\partial U(q_i(t + \epsilon))} {\partial q_i} \end{align}\]
Preserves volume exactly
Reversible
We don’t get exact invariance (so probability of acceptance is not 1)
Step size and number of steps is still important!

MCMC with HMC

Steps: replace \(\mathbf{q}\) with \(\boldsymbol{\theta}\)

sample a new value for the momentum \(\mathbf{p}^{(t)} \sim \textsf{N}(\mathbf{0}_K, \mathbf{M})\)
Metropolis: from current state \((\mathbf{q}^{(t-1)}, \mathbf{p}^{(t)})\) simulate proposal \((\mathbf{q}^*, \mathbf{p}^*)\) using Hamiltonian dynamics by applying Leapfrog with step size \(\epsilon\) for \(L\) steps (tuning parameters) (start with \(\epsilon*L = 1\))
Accept or reject acceptance probability is \[\min \{1, \exp( - \cal{H}(\mathbf{q}^*, \mathbf{p}^*) + \cal{H}(\mathbf{q}^{(t-1)}, \mathbf{p}^{(t)}) \}\] . . .

theory suggests optimal acceptance rate is around 65%

Tuning

in addition to tuning \(\epsilon\) and \(L\), we can tune \(\mathbf{M}\)
\(\text{Cov}(\mathbf{q}) = \mathbf{V}\) can be highly variable
Consider reparameterization \(\mathbf{A}\mathbf{q} = \mathbf{q}^\prime\) so that \(\text{Cov}(\mathbf{A}\mathbf{q}) = \mathbf{A}\mathbf{V}\mathbf{A}^T = \mathbf{I}_d\); \(\mathbf{A}= \mathbf{V}^{-1/2}\)
eliminates posterior correlation!
general trick of reparameterizing to reduce posterior correlation is often called pre-conditioning - improves efficiency!
use \(\mathbf{M}= \mathbf{I}_d\)
Automatic tuning is achieved by the No-U-Turn-Sampler (NUTS) (bit complicated, but used by STAN)
other variations Metropolis-Adjusted Langevin Algorithm (MALA)

Hybrid Approaches

Recall mixed effects model \[Y_{ij} = \mathbf{x}_{ij}^T \boldsymbol{\beta}+ \mathbf{z}_{ij}^T \boldsymbol{\gamma}_j + \epsilon_{ij} \qquad \epsilon_{ij} \sim \textsf{N}(0, \sigma^2)\]
random effects \(\boldsymbol{\gamma}_j \sim \textsf{N}_d(\mathbf{0}_d, \boldsymbol{\Psi})\) (diagonal \(\boldsymbol{\Psi}\))
marginalize over the random effects \[\mathbf{Y}_{j} = \textsf{N}(\mathbf{X}_j \boldsymbol{\beta}, \mathbf{Z}_j \boldsymbol{\Psi}\mathbf{Z}_j^T + \sigma^2 \mathbf{I}_{n_j})\]
we could use Gibbs on the conditional model, but we may get slow mixing (i.e. due to updating variance components)
run HMC within Gibbs to update the variance components \(\boldsymbol{\Psi}\) and \(\sigma^2\) using the marginal model given \(\boldsymbol{\beta}\)
HMC in its basic form doesn’t like constraints so reparameterize to use log transformations

Advantages & Disadvantages

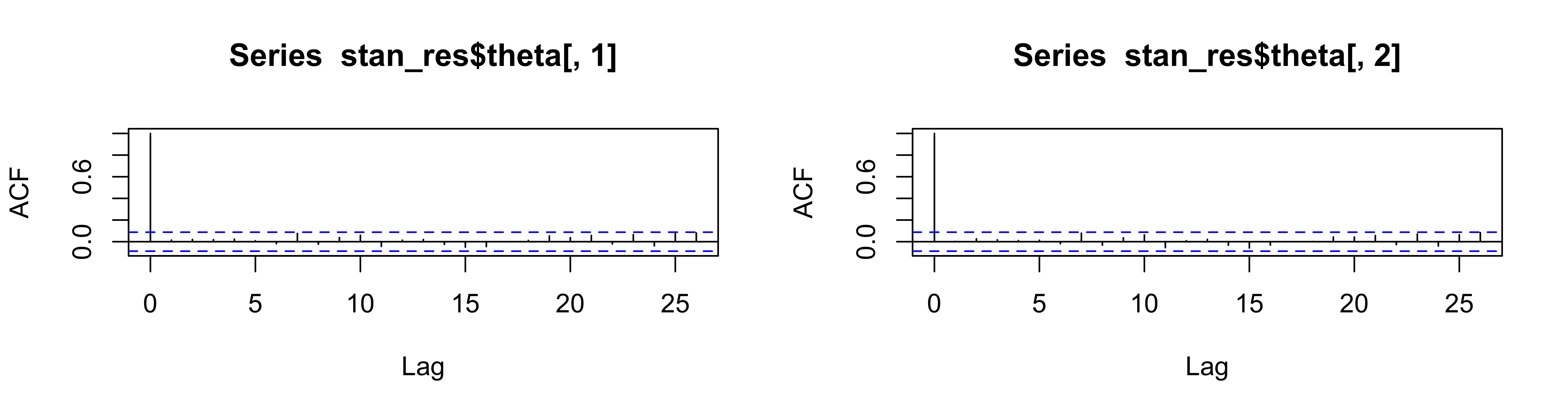
HMC can produce samples with low correlation and high acceptance ratio!
can be slow with long or short tailed distributions (use local curvature in \(\mathbf{M}\))
driven by step size (larger time steps mean values are farther away but may lead to lower acceptance- error is \(O(\epsilon^2)\) for the leapfrog method)
number of steps (more steps reduces correlation; to avoid U turns stan uses NUTS)
most implementations limited to continuous variables (need gradients of log densities)
need to calculate gradients (analytic or automatic differentiation methods)
can mix Gibbs (for discrete) and HMC (for continuous)
Nishimura et al (2020 Biometrika) for HMC with discrete targets
rates of convergence and other theory