Lecture 19: Random Effects

STA702

Merlise Clyde

Duke University

Building Hierarchical Models

Models for Gaussian Data with no Covariates \[ y_{ij} \sim \, ? \qquad i = 1, \ldots n_j; j = 1, \ldots, J\]
\(j\) blocking variable - schools, counties, etc (categorical)
\(i\) observations within a block - students within schools, households within counties, etc
potentially there may be within block dependence in the observations due to unmeasured covariates
structure?

Models

Naive model (baseline) \[ y_{ij} \overset{iid}{\sim} N(\mu, \sigma^2) \]
issue: no systematic variation across blocks
Fixed Effects model: \[ y_{ij} \overset{ind}{\sim} N(\mu_j, \sigma^2) \]
Common reparameterization \[ y_{ij} \overset{ind}{\sim} N(\alpha + \beta_j, \sigma^2) \]
\(\mu\) intercept
\(\beta_j\) shift for school
Identifiability ?

Non-Identifiability

Example: \(y_{ij} \sim N(\alpha + \beta_j, \sigma^2)\) overparameterized
\(\mu_j = \alpha + \beta_j\) and \(\sigma^2\) are uniquely estimated, but not \(\alpha\) or \(\beta_j\)
\(x_{ij} \in \{1, \ldots, J \}\) factor levels \[y_{ij} \sim N(\alpha+ \sum_{j^\prime}\beta_j 1(x_{ij^{\prime}} = j), \sigma^2)\]
\(\mu_j = \alpha + \beta_j\) identifiable - \(J\) equations but \(J + 1\) unknowns
Put constraints on parameters
- \(\alpha = 0\)
- \(\beta_J = 0\)
- \(\sum \beta_j = 0\)

Bayesian Notion of Identifiability

Bayesian Learning
model is likelihood and prior
the posterior distribution differs from the prior

Note:

Priors may lead to posteriors where parameters are identifiable even if not under likelihood
Forcing identifiability may involve (complex) constraints that bias parameter estimates \[ \begin{align} \alpha & \sim \textsf{N}(0, \sigma^2_\alpha) \\ \beta_j & \mathrel{\mathop{\sim}\limits^{\rm iid}}\textsf{N}(0, \sigma^2_\beta) \text{ for } j = 1, \ldots, J-1 \\ \mu_J & \sim \textsf{N}(0, \sigma^2_\alpha) \\ \mu_j &\ iid \textsf{N}(0, \sigma^2_\alpha + \sigma^2_\beta) \text{ for } j = 1, \ldots, J-1 \end{align} \]
sometimes purposely introduce non-identifiability to improve computation (parameter expansion PX)
run non-identifiable model and focus on identifiable parameters or functions of them

Issue with Fixed Effect Approach

What if \(n_i\), number of observations per block, are small?
Estimated uncertainty/variances are large based on MLE using group specific means
What if blocks might be viewed as a sample from some larger population? Sample of schools?
May want inference about the larger population and say things about future blocks (schools) !
fixed effects do not allow us to say anything about blocks not in our sample!
how to address this?

Random Effects

\[\begin{align*} y_{ij} & = \alpha + \beta_i + \epsilon_{ij}, \qquad \epsilon_{ij} \overset{iid}{\sim} N(0, \sigma^2) \\ \beta_i & \overset{iid}{\sim} N(0, \tau^2) \end{align*}\]

random effects \(\beta_j\)

Note: Don’t confuse random effect distributions with prior distributions!

Random effect distributions should be viewed as part of the model specification
We’ve specified the likelihood in a hierarchical manner to induce desirable structure
unknown parameters are population parameters \(\alpha\), \(\tau\) and \(\sigma^2\)
Bayesians put prior distributions on \(\alpha\), \(\tau\) and \(\sigma^2\); frequentists don’t!

Equivalent Model

\[y_{j} = (y_{1j}, y_{2j}, \ldots, y_{n_j j})\] \[y_j \mid \alpha, \sigma^2, \tau^2 \mathrel{\mathop{\sim}\limits^{\rm ind}}N_{n_j}\left( \mathbf{1}_{n_j} \alpha, \left( \begin{array}{cccc} \sigma^2 + \tau^2 & \tau^2 & \ldots & \tau^2 \\ \tau^2 & \ddots & & \tau^2 \\ \vdots & & \ddots & \vdots \\ \tau^2 & \ldots & \tau^2 & \sigma^2 + \tau^2 \end{array}\right) \right)\]

within-block correlation constant
algorithmically we can use either the latent variable model or the collapsed (marginal) model for inferences;
often latent variable is easier to work with for Bayes!
MLEs of \(\tau\) on boundary in some cases!

Simple Gibbs Sampler

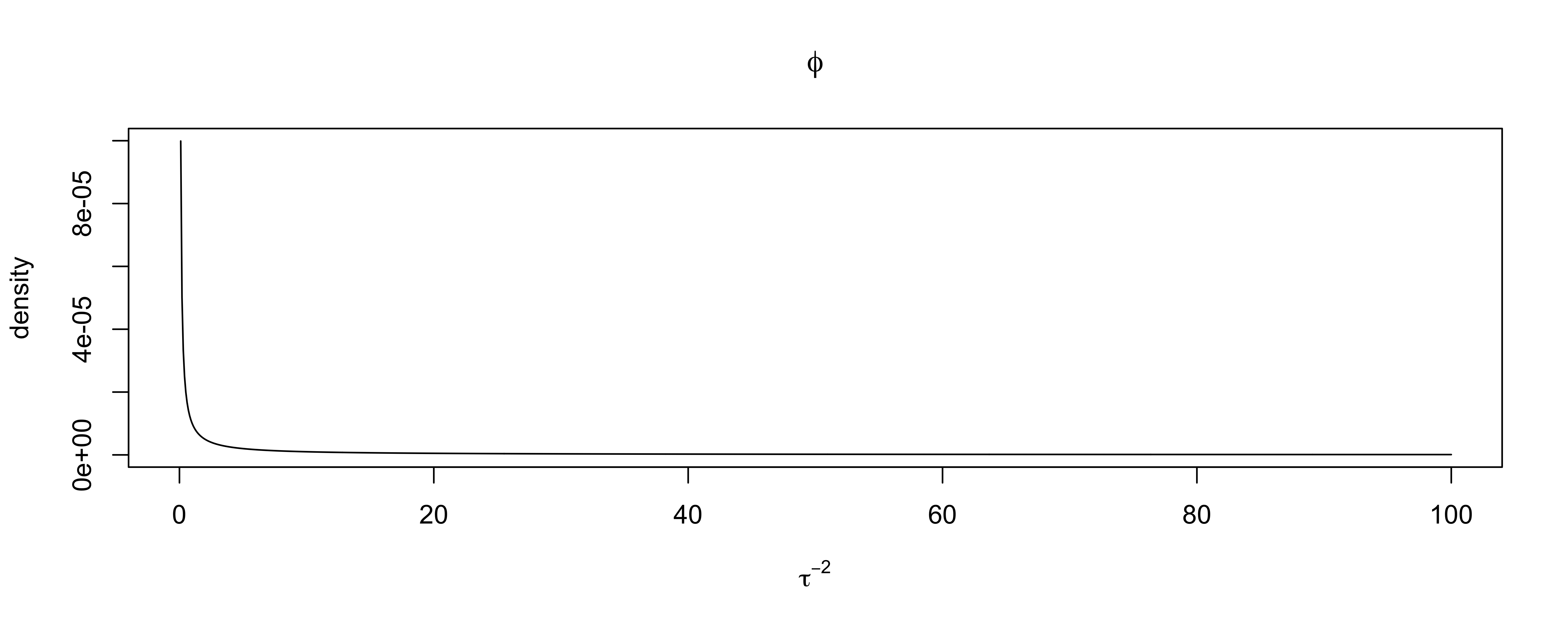
Reparameterize \(\theta = (\alpha, \phi_\tau = 1/\tau^2, \phi_\sigma = 1/\sigma^2, \beta_1, \ldots, \beta_J)\)
Priors (parameters Greek letters, hyperparameters Roman) \[\begin{align*} \alpha & \sim \textsf{N}(a_0, 1/P_0) \\ \phi_\tau & \sim \textsf{Gamma}(a_\tau/2, b_\tau/2) \\ \phi_\sigma & \sim \textsf{Gamma}(a_\sigma/2, b_\sigma/2) \end{align*}\]
Full Conditional for \(\alpha\) \[\begin{align*}\alpha \mid \tau^2, \sigma^2, \beta_1, \ldots \beta_n & \sim \textsf{N}(a_n, 1/P_n) \\ P_n = \left(P_0 + \sum_j n_{j} \phi_\sigma \right) & \quad a_n = \frac{a_0 P_0 + \sum_j n_j \bar{y}^*_j }{P_n} \\ \bar{y}^*_j & \equiv \frac{\sum_i (y_{ij} - \beta_j)}{n_j} \end{align*}\]

Full Conditionals Continued

\[\begin{align*} \phi_\sigma \mid \alpha, \phi_\tau, \beta_1, \ldots, \beta_J \sim \textsf{Gamma}\left(\frac{a_\sigma + \sum_j n_j}{2}, \frac{b_\sigma + \sum_{ij} (y_{ij} - \alpha - \beta_j)^2}{2} \right) \end{align*}\]

\[\begin{align*}\beta_j \mid \alpha, \tau, \sigma^2 & \mathrel{\mathop{\sim}\limits^{\rm ind}}\textsf{N}( \hat{b}_j, \hat{P}_{\beta_j}^{-1}) \\ \hat{P}_{\beta_j} &= \left(\phi_\tau + n_j \phi_\sigma \right) \\ \hat{b}_j & = \frac{\phi_{\tau} + n_j \phi_\sigma \bar{y}^{**}_j }{\hat{P}_{\beta_j}} \\ \bar{y}^{**}_j & \equiv \frac{\sum_i (y_{ij} - \alpha)}{n_j} \end{align*}\]

\[\begin{align*} \phi_\tau \mid \alpha, \sigma^2, \beta_1, \ldots, \beta_J \sim \textsf{Gamma}\left(\frac{a_\tau + J}{2}, \frac{b_\tau+ \sum_j \beta_j^2}{2} \right) \end{align*}\]

Complications Relative to Usual Regression

Prior Choice
Mixing and its dependence on parameterization

Early recommendation after Gibbs Sampler used non-informative priors \[\begin{align*} \pi(\alpha) & \propto 1 \\ \pi(\phi_\sigma) & \sim \textsf{Gamma}(\epsilon/2, \epsilon/2) \qquad \pi(\phi_\sigma ) \propto 1/\phi_\sigma \text{ as } \epsilon \to 0 \\ \pi(\phi_\tau) & \sim \textsf{Gamma}(\epsilon/2, \epsilon/2) \qquad \pi(\phi_\tau) \propto 1/\phi_\tau \text{ as } \epsilon \to 0 \end{align*}\]
Are full conditionals proper ?
Is joint posterior proper ?

MCMC and Improper Priors

proper full conditionals even with improper priors
but joint is improper !
MCMC won’t converge to the stationary distribution (doesn’t exist)
may not notice it!
Hill (1965) considered the one-way anova model and showed impropriety for \(p(\tau^2) \propto 1/\tau^2\)
Hobart & Casella (1996) provide conditions on improper priors leading to proper posteriors in more general random and mixed effects models

Diffuse But Proper

\[\begin{align*} \alpha & \sim N(0, 10^{-6})\\ \pi(\phi_\sigma) & \sim \textsf{Gamma}(10^{-6}, 10^{-6} )\\ \pi(\phi_\tau) & \sim \textsf{Gamma}(10^{-6}, 10^{-6} ) \end{align*}\]

Nearly improper priors may lead to terrible performance! highly sensitive to just how vague the prior is! (Domains of attraction)

Alternative Priors

\[\begin{align*} y_{ij} \mid \alpha, \beta_1, \ldots \beta_J, \phi_\sigma^2 & \mathrel{\mathop{\sim}\limits^{\rm ind}}\textsf{N}(\alpha + \beta_j, 1/\phi_\sigma^2) \\ p(\alpha, \phi_\sigma) & \propto 1/\phi_\sigma \\ \beta_j \mid \tau & \overset{iid}{\sim} \textsf{N}(0, \tau^2) \end{align*}\]

Gelman 2006 in a discussion of Browne & Draper paper in Bayesian Analysis recommended priors on random effect standard deviation \(\tau\)
\(\pi(\tau ) \propto 1(\tau > 0)\) (improper prior on sd)
\(\pi(\tau ) \propto 1(\tau > 0)\textsf{N}(0,1)\) folded standard normal (half-normal)
\(\pi(\tau ) \propto 1(\tau > 0)\textsf{N}(0,1/\psi) \qquad \psi \sim \textsf{Gamma}(\nu/2, \nu/2)\) leads to a folded t or half t with \(\nu\) degrees of freedom marginally

Proper Posterior ?

Integrate out \(\beta_j\) and work with
\[\pi(\mu, \tau, \sigma^2 \mid y) \propto \pi(\mu, \tau, \sigma^2) \prod_{j=1}^J \textsf{N}\left(y_{j}; \mathbf{1}_{n_j} \alpha, \left( \begin{array}{cccc} \sigma^2 + \tau^2 & \tau^2 & \ldots & \tau^2 \\ \tau^2 & \ddots & & \tau^2 \\ \vdots & & \ddots & \vdots \\ \tau^2 & \ldots & \tau^2 & \sigma^2 + \tau^2 \end{array}\right) \right)\]

take \(\pi(\mu, \tau, \sigma^2) \propto \sigma^{-2} \, \textsf{C}^+(\tau; 0, 1)\)

take \(\pi(\mu, \tau, \sigma^2) \propto \sigma^{-2}\) (note prior on standard deviation \(\tau\))
Is joint posterior is proper ? (see Hobart & Casella)

Propriety

expression for marginal likelihood requires determinant and inverse of intra-class correlation matrix!
Write covariance as \(\sigma^2 \mathbf{I}_{n_j} + \tau^2 n_j \mathbf{P}_{\mathbf{1}_{n_j}}\) and find spectral decomposition \[\begin{align} \sigma^2 \mathbf{I}_{n_j} + \tau^2 n_j \mathbf{P}_{\mathbf{1}_{n_j}} & = \mathbf{U}[\sigma^2 \mathbf{I}_{n_j} + \tau^2 n_j \text{diag}(1, 0 , \ldots, 0)] \mathbf{U}^T\\ (\sigma^2 \mathbf{I}_{n_j} + \tau^2 n_j \mathbf{P}_{\mathbf{1}_{n_j}} )^{-1} & = \frac{1}{\sigma^2} (\mathbf{I}_{n_j} + \frac{\tau^2 n_j}{\sigma^2 + \tau^2 n_j} \mathbf{P}_{\mathbf{1}_{n_j}}) \end{align}\]
integrate out \(\alpha\) (messy completing the square)! see Hill 1965 Equation 3.
consider conditional distributions from \(1/\sigma^2\) and \(\tau\)
determine if integrals are finite (what happens at \(\tau\) near 0 ?)
look at special case when \(n_j\) are all equal

Bayes Estimates of Variances

Avoids issues when estimate of variance is on the boundary of the parmaeter space
Do not have to use asymptotics to construct CI!
full uncertainty propagation
predictive distributions for future data
Gelman (2006) recommends half-t if the number of groups is small or uniform but uniform on the standard deviation \(\tau\) does lead to an improper posterior if \(J \leq 3\)
Hobart & Casella (1996) provides more rigorous conditions with improper priors