Lecture 13: Ridge Regression, Lasso and Mixture Priors

STA702

Merlise Clyde

Duke University

Ridge Regression

Model: \(\mathbf{Y}= \mathbf{1}_n \alpha + \mathbf{X}\boldsymbol{\beta}+ \boldsymbol{\epsilon}\)

• typically expect the intercept \(\alpha\) to be a different order of magnitude from the other predictors. Adopt a two block prior with \(p(\alpha) \propto 1\)

• Prior \(\boldsymbol{\beta}\mid \phi \sim \textsf{N}(\mathbf{0}_b, \frac{1} {\phi \kappa} \mathbf{I}_p\)) implies the \(\boldsymbol{\beta}\) are exchangable a priori (i.e. distribution is invariant under permuting the labels and with a common scale and mean)

• Posterior for \(\boldsymbol{\beta}\) \[\boldsymbol{\beta}\mid \phi, \kappa, \mathbf{Y}\sim \textsf{N}\left((\kappa I_p + X^TX)^{-1} X^T Y, \frac{1}{\phi}(\kappa I_p + X^TX)^{-1} \right)\]

• assume that \(\mathbf{X}\) has been centered and scaled so that \(\mathbf{X}^T\mathbf{X}= \textsf{corr}(\mathbf{X})\) and \(\mathbf{1}_n^T \mathbf{X}= \mathbf{0}_p\)

X = scale(X)/sqrt{nrow(X) - 1}

Bayes Ridge Regression

• related to penalized maximum likelihood estimation \[-\frac{\phi}{2}\left(\|\mathbf{Y}- \mathbf{X}\boldsymbol{\beta}\|^2 + \kappa \| \boldsymbol{\beta}\|^2 \right) \]

• frequentist’s expected mean squared error loss for using \(\mathbf{b}_n\) \[\textsf{E}_{\mathbf{Y}\mid \boldsymbol{\beta}_*}[\| \mathbf{b}_n - \boldsymbol{\beta}_* \|^2] = \sigma^2 \sum_{j = 1}^2 \frac{\lambda_j}{(\lambda_j + \kappa)^2} + \kappa^2 \boldsymbol{\beta}_*^T(\mathbf{X}^T\mathbf{X}+ \kappa \mathbf{I}_p)^{-2} \boldsymbol{\beta}_*\]

• eigenvalues of \(\mathbf{X}^T\mathbf{X}= \mathbf{V}\boldsymbol{\Lambda}\mathbf{V}^T\) with \([\boldsymbol{\Lambda}]_{jj} = \lambda_j\)

• can show that there always is a value of \(\kappa\) where is smaller for the (Bayes) Ridge estimator than MLE

• Unfortunately the optimal choice depends on “true” \(\boldsymbol{\beta}_*\)!

• orthogonal \(\mathbf{X}\) leads to James-Stein solution related to Empirical Bayes

Choice of \(\kappa\)?

• fixed a priori Bayes (and how to choose?)
  

• Cross-validation (frequentist)

• Empirical Bayes? (frequentist/Bayes)

• Should there be a common \(\kappa\)? (same shrinkage across all variables?)

• Or a \(\kappa_j\) per variable? (or shared among a group of variables (eg. factors) ?)

• Treat as unknown!

Mixture of Conjugate Priors

• can place a prior on \(\kappa\) or \(\kappa_j\) for fully Bayes

• similar option for \(g\) in the \(g\) priors

• often improved robustness over fixed choices of hyperparameter

• may not have cloosed form posterior but sampling is still often easy!

• Examples:

  • Bayesian Lasso (Park & Casella, Hans)
  • Generalized Double Pareto (Armagan, Dunson & Lee)
  • Horseshoe (Carvalho, Polson & Scott)
  • Normal-Exponential-Gamma (Griffen & Brown)
  • mixtures of \(g\)-priors (Liang et al)

Lasso

Tibshirani (JRSS B 1996) proposed estimating coefficients through \(L_1\) constrained least squares ``Least Absolute Shrinkage and Selection Operator’’

• Control how large coefficients may grow \[\begin{align} \min_{\boldsymbol{\beta}} & \| \mathbf{Y}- \mathbf{1}_n \alpha - \mathbf{X}\boldsymbol{\beta}\|^2 \\ & \textsf{ subject to } \sum |\beta_j| \le t \end{align}\]

• Equivalent Quadratic Programming Problem for ``penalized’’ Likelihood \[\min_{\boldsymbol{\beta}} \| \mathbf{Y}- \mathbf{1}_n \alpha - \mathbf{X}\boldsymbol{\beta}\|^2 + \lambda \|\boldsymbol{\beta}\|_1\]

• Equivalent to finding posterior mode \[ \max_{\boldsymbol{\beta}} -\frac{\phi}{2} \{ \| \mathbf{Y}- \mathbf{1}_n \alpha - \mathbf{X}\boldsymbol{\beta}\|^2 + \lambda \|\boldsymbol{\beta}\|_1 \} \]

Bayesian Lasso

Park & Casella (JASA 2008) and Hans (Biometrika 2010) propose Bayesian versions of the Lasso
\[\begin{eqnarray*} \mathbf{Y}\mid \alpha, \boldsymbol{\beta}, \phi & \sim & \textsf{N}(\mathbf{1}_n \alpha + \mathbf{X}\boldsymbol{\beta}, \mathbf{I}_n/\phi) \\ \boldsymbol{\beta}\mid \alpha, \phi, \boldsymbol{\tau}& \sim & \textsf{N}(\mathbf{0}, \textsf{diag}(\boldsymbol{\tau}^2)/\phi) \\ \tau_1^2 \ldots, \tau_p^2 \mid \alpha, \phi & \mathrel{\mathop{\sim}\limits^{\rm iid}}& \textsf{Exp}(\lambda^2/2) \\ p(\alpha, \phi) & \propto& 1/\phi \\ \end{eqnarray*}\]

• Can show that \(\beta_j \mid \phi, \lambda \mathrel{\mathop{\sim}\limits^{\rm iid}}DE(\lambda \sqrt{\phi})\) \[\int_0^\infty \frac{1}{\sqrt{2 \pi s}} e^{-\frac{1}{2} \phi \frac{\beta^2}{s }} \, \frac{\lambda^2}{2} e^{- \frac{\lambda^2 s}{2}}\, ds = \frac{\lambda \phi^{1/2}}{2} e^{-\lambda \phi^{1/2} |\beta|} \]

• equivalent to penalized regression with \(\lambda^* = \lambda/\phi^{1/2}\)

• Scale Mixture of Normals (Andrews and Mallows 1974)

Gibbs Sampling

• Integrate out \(\alpha\): \(\alpha \mid \mathbf{Y}, \phi \sim \textsf{N}(\bar{y}, 1/(n \phi)\)
  

• \(\boldsymbol{\beta}\mid \boldsymbol{\tau}, \phi, \lambda, \mathbf{Y}\sim \textsf{N}(, )\)
  

• \(\phi \mid \boldsymbol{\tau}, \boldsymbol{\beta}, \lambda, \mathbf{Y}\sim \mathbf{G}( , )\)
  

• \(1/\tau_j^2 \mid \boldsymbol{\beta}, \phi, \lambda, \mathbf{Y}\sim \textsf{InvGaussian}( , )\)

• For \(X \sim \textsf{InvGaussian}(\mu, \lambda)\), the density is \[ f(x) = \sqrt{\frac{\lambda^2}{2 \pi}} x^{-3/2} e^{- \frac{1}{2} \frac{ \lambda^2( x - \mu)^2} {\mu^2 x}} \qquad x > 0 \]

Homework

Derive the full conditionals for \(\boldsymbol{\beta}\), \(\phi\), \(1/\tau^2\) for the model in Park & Casella

Choice of Estimator

• Posterior mode (like in the LASSO) may set some coefficients exactly to zero leading to variable selection - optimization problem (quadratic programming)

• Posterior distribution for \(\beta_j\) does not assign any probability to \(\beta_j = 0\) so posterior mean results in no selection, but shrinkage of coeffiecients to prior mean of zero

• In both cases, large coefficients may be over-shrunk (true for LASSO too)!

• Issue is that the tails of the prior under the double exponential are not heavier than the normal likelihood

• Only one parameter \(\lambda\) that controls shrinkage and selection (with the mode)

• Need priors with heavier tails than the normal!!!

Shrinkage Comparison with Posterior Mean

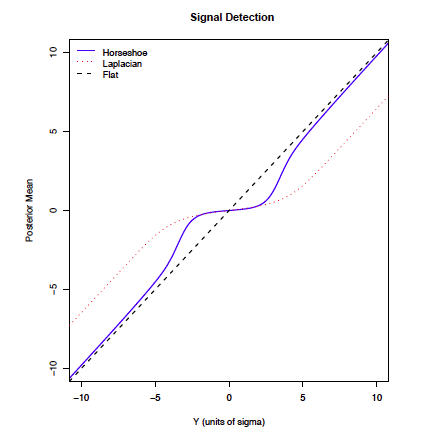
HS - Horseshoe of Carvalho, Polson & Scott (slight difference in CPS notation)

\[\begin{align} \boldsymbol{\beta}\mid \phi, \boldsymbol{\tau}& \sim \textsf{N}(\mathbf{0}_p, \frac{\textsf{diag}(\boldsymbol{\tau}^2)}{ \phi }) \\ \tau_j \mid \lambda & \mathrel{\mathop{\sim}\limits^{\rm iid}}\textsf{C}^+(0, \lambda^2) \\ \lambda & \sim \textsf{C}^+(0, 1) \\ p(\alpha, \phi) & \propto 1/\phi) \end{align}\]

• resulting prior on \(\boldsymbol{\beta}\) has heavy tails like a Cauchy!

Bounded Influence for Mean

• canonical representation (normal means problem) \(\mathbf{Y}= \mathbf{I}_p \boldsymbol{\beta}+ \boldsymbol{\epsilon}\) so \(\hat{\beta}_i = y_i\) \[ E[\beta_i \mid \mathbf{Y}] = \int_0^1 (1 - \psi_i) y^*_i p(\psi_i \mid \mathbf{Y})\ d\psi_i = (1 - \textsf{E}[\psi_i \mid y^*_i]) y^*_i\]

• \(\psi_i = 1/(1 + \tau_i^2)\) shrinkage factor

• Posterior mean \(E[\beta \mid y] = y + \frac{d} {d y} \log m(y)\) where \(m(y)\) is the predictive density under the prior (known \(\lambda\))

• Bounded Influence: if \(\lim_{|y| \to \infty} \frac{d}{dy} \log m(y) = c\) (for some constant \(c\))

• HS has bounded influence where \(c = 0\) so \[\lim_{|y| \to \infty} E[\beta \mid y) \to y \]

• DE has bounded influence but \((c \ne 0\)); bound does not decay to zero and bias for large \(|y_i|\)

Properties for Shrinkage and Selection

Fan & Li (JASA 2001) discuss Variable Selection via Nonconcave Penalties and Oracle Properties

• Model \(Y = \mathbf{1}_n \alpha + \mathbf{X}\boldsymbol{\beta}+ \boldsymbol{\epsilon}\) with \(\mathbf{X}^T\mathbf{X}= \mathbf{I}_p\) (orthonormal) and \(\boldsymbol{\epsilon}\sim N(0, \mathbf{I}_n)\)

• Penalized Log Likelihood \[\frac 1 2 \|\mathbf{Y}- \hat{\mathbf{Y}}\|^2 +\frac 1 2 \sum_j(\beta_j - \hat{\beta}_j)^2 + \sum_j \text{ pen}_\lambda(|\beta_j|)\]

• duality \(\text{pen}_\lambda(|\beta|) \equiv - \log(p(|\beta_j|))\) (negative log prior)

• Objectives:

  • Unbiasedness: for large \(|\beta_j|\)
  • Sparsity: thresholding rule sets small coefficients to 0
  • Continuity: continuous in \(\hat{\beta}_j\)

Conditions on Prior/Penalty

Derivative of \(\frac 1 2 \sum_j(\beta_j - \hat{\beta}_j)^2 + \sum_j \text{pen}_\lambda(|\beta_j|)\) is \(\mathop{\mathrm{sgn}}(\beta_j)\left\{|\beta_j| + \text{pen}^\prime_\lambda(|\beta_j|) \right\} - \hat{\beta}_j\)

• Conditions:

  • unbiased: if \(\text{pen}^\prime_\lambda(|\beta|) = 0\) for large \(|\beta|\); estimator is \(\hat{\beta}_j\)

  • thresholding: \(\min \left\{ |\beta_j| + \text{pen}^\prime_\lambda(|\beta_j|)\right\} > 0\) then estimator is 0 if \(|\hat{\beta}_j| < \min \left\{ |\beta_j| + \text{pen}^\prime_\lambda(|\beta_j|) \right\}\)

  • continuity: minimum of \(|\beta_j| + \text{pen}^\prime_\lambda(|\beta_j|)\) is at zero

• Can show that LASSO/ Bayesian Lasso fails conditions for unbiasedness

• What about other Bayes methods?

Homework

Check the conditions for the DE, Generalized Double Pareto and Cauchy priors

Selection

• Only get variable selection if we use the posterior mode

• If selection is a goal of analysis build it into the model/analysis/post-analysis

  • prior belief that coefficient is zero

  • selection solved as a post-analysis decision problem

• Even if selection is not an objective, account for the uncertainty that some predictors may be unrelated