Prior/Posterior Checks

STA 702: Lecture 4

Merlise Clyde

Duke University

Uses of Posterior Predictive

• Plot the entire density or summarize

• Available analytically for conjugate families

• Monte Carlo Approximation \[p(y_{n+1} \mid y_1, \ldots y_n) \approx \frac 1 T \sum_{t = 1}^T p(y_{n+1} \mid \theta^{(t)})\] where \(\theta^{(t)} \sim \pi(\theta \mid y_1, \ldots y_n)\) for \(t = 1, \ldots, T\)

• T samples from the posterior distribution

• Empirical Estimates & Quantiles from Monte Carlo Samples

Models

• So far this all assumes we have a correct sampling model and a “reasonable” prior distrbution

• George Box: All models are wrong but some are useful

• “Useful” \(\rightarrow\) model provides a good approximation; there aren’t clear aspects of the data that are ignored or misspecified

• how can we decide if a model is misspecified and needs to change?

Example

• Poisson model \[Y_i \mid \theta \stackrel{iid}{\sim }\textsf{Poisson}(\theta) \qquad i = 1, \ldots, n\]

• How might our model be misspecified?

  • Poisson assumes that \(\textsf{E}(Y_i) = \textsf{Var}(Y_i) = \theta\)

  • it’s very common for data to be over-dispersed \(\textsf{E}(Y_i) < \textsf{Var}(Y_i)\)

  • ignored additional structure in the data, i.e. data are not iid

  • zero-inflation many more zero values than consistent with the poisson model

Posterior Predictive Checks

• Guttman (1967), Rubin (1984) proposed the use of Posterior Predictive Checks (PPC)] for model criticism; further developed by Gelman et al (1996)

• the spirit of posterior predictive checks is that “If my model is good, then its posterior predictive distribution will generate data that look like my oberved data”

• \(y^{\text{obs}}\) is the observed data

• \(y^{\text{rep}}\) is a new dataset sampled from the posterior predictive \(p(y^{\text{rep}} \mid y^{\text{obs}})\) of size \(n\) (same size as the observed)

• Use a diagnostic statistic \(d(y)\) to capture some feature of the data that the model may fail to capture, say variance

• compare \(d(y^{\text{obs}})\) to the reference distribution of \(d(y^{\text{rep}})\)

• Use Posterior Predictive P-value as a summary \[ p_{PPC} = P(d(y^{\text{obs}}) > d(y^{\text{rep}}) \mid y^{\text{obs}}) \]

Formally

• choose a “diagnostic statistic” \(d(\cdot)\) that captures some summary of the data, e.g. \(\textsf{Var}(y)\) for over-dispersion, where large values of the statistic would be surprising if the model were correct.

• \(d(y^{\text{obs}}) \equiv d_{\textrm{obs}}\) value of statistic in observed data

• \(d(y^{\text{rep}}_t) \equiv d_{\textrm{pred}}\) value of statistic for the \(t\)th random dataset drawn from the posterior predictive distribution

  1. Generate \(\theta_t \stackrel{iid}{\sim}p(\theta \mid y^{\textrm{obs}})\)
  2. Generate \(y^{\textrm{rep}_t} \mid \theta_t \stackrel{iid}{\sim} p(y \mid \theta_t)\)
  3. Calculate \(d(y^{\text{rep}}_t)\)

• plot posterior predictive distribution of \(d(y^{\text{rep}}_t)\) and add \(d_{\textrm{obs}}\)

• How extreme is \(t_{\textrm{obs}}\) compared to the distribution of \(d(y^{\text{rep}})\)?

• compute p-value \(p_{PPC} = \frac 1 T \sum_t I(d(y^{\text{obs}}) > d(y^{\text{rep}}_t))\)

Example with Over Dispersion

n = 100; phi = 1; mu = 5
theta.t = rgamma(n,phi,phi/mu)
y = rpois(n, theta.t)
a = 1; b = 1;
t.obs = var(y)

nT = 10000
t.pred = rep(NA, nT)
for (t in 1:nT) {
  theta.post = rgamma(1, a + sum(y),
                         b + n)
  y.pred = rpois(n, theta.post)
  t.pred[t] = var(y.pred)
}

hist(t.pred, 
     xlim = range(c(t.pred, t.obs)),
     xlab="var", 
     main="Posterior Predictive Distribution")

abline(v = t.obs, col="red")

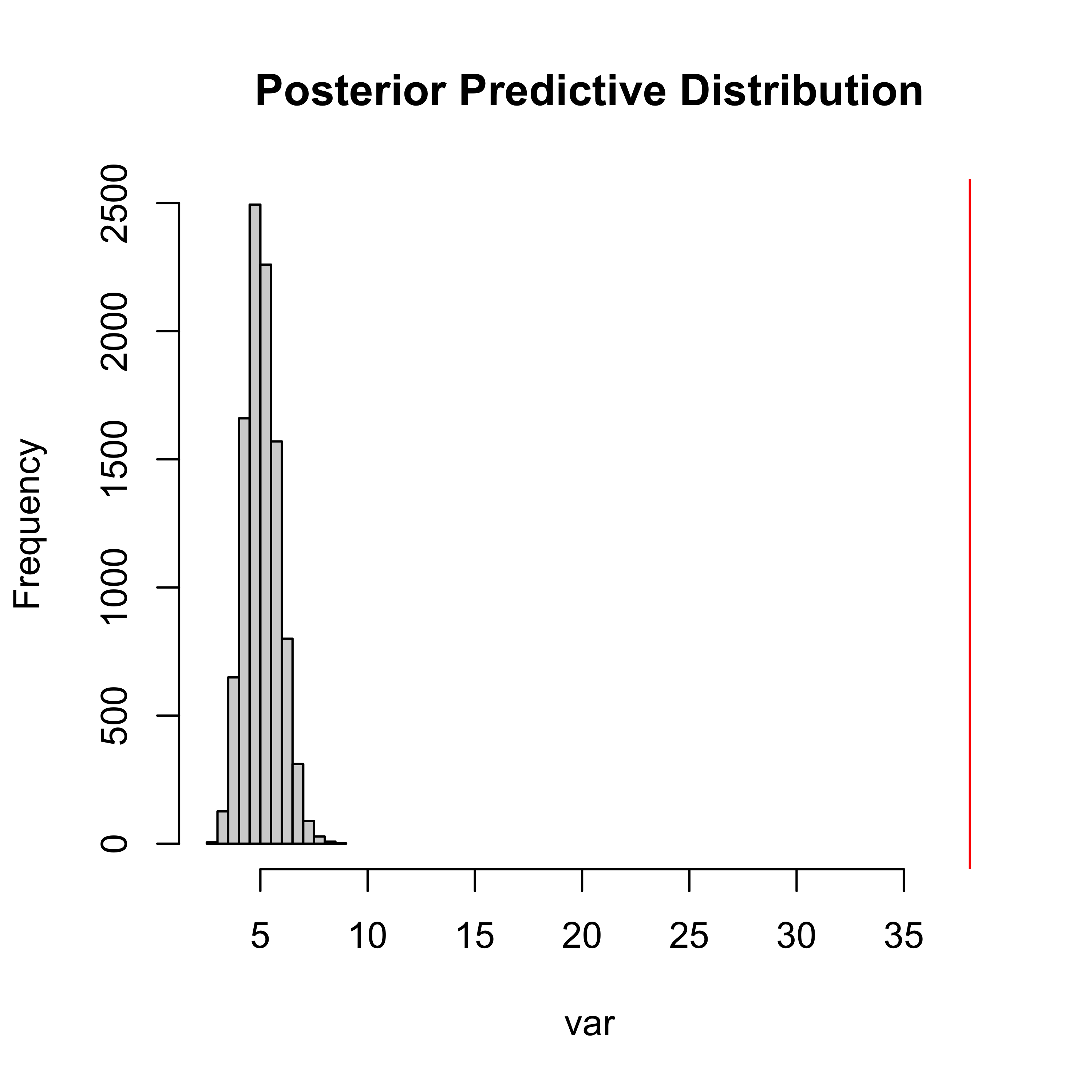
Zero Inflated Distribution

R Code to generate zero inflated

n = 1000
mu = 5; phi = 1
theta.t = rgamma(n,phi,phi/mu)
z = rbinom(n, 1, .90)
y = rpois(n, theta.t)*z

• Let the \(d()\) be the proportion of zeros in the sample \[\begin{aligned} d(y) & = \frac{\sum_{i = 1}^{n}1(y_i = 0)}{n} \\ & = 0.24 \end{aligned}\]
  

Posterior Predictive Distribution

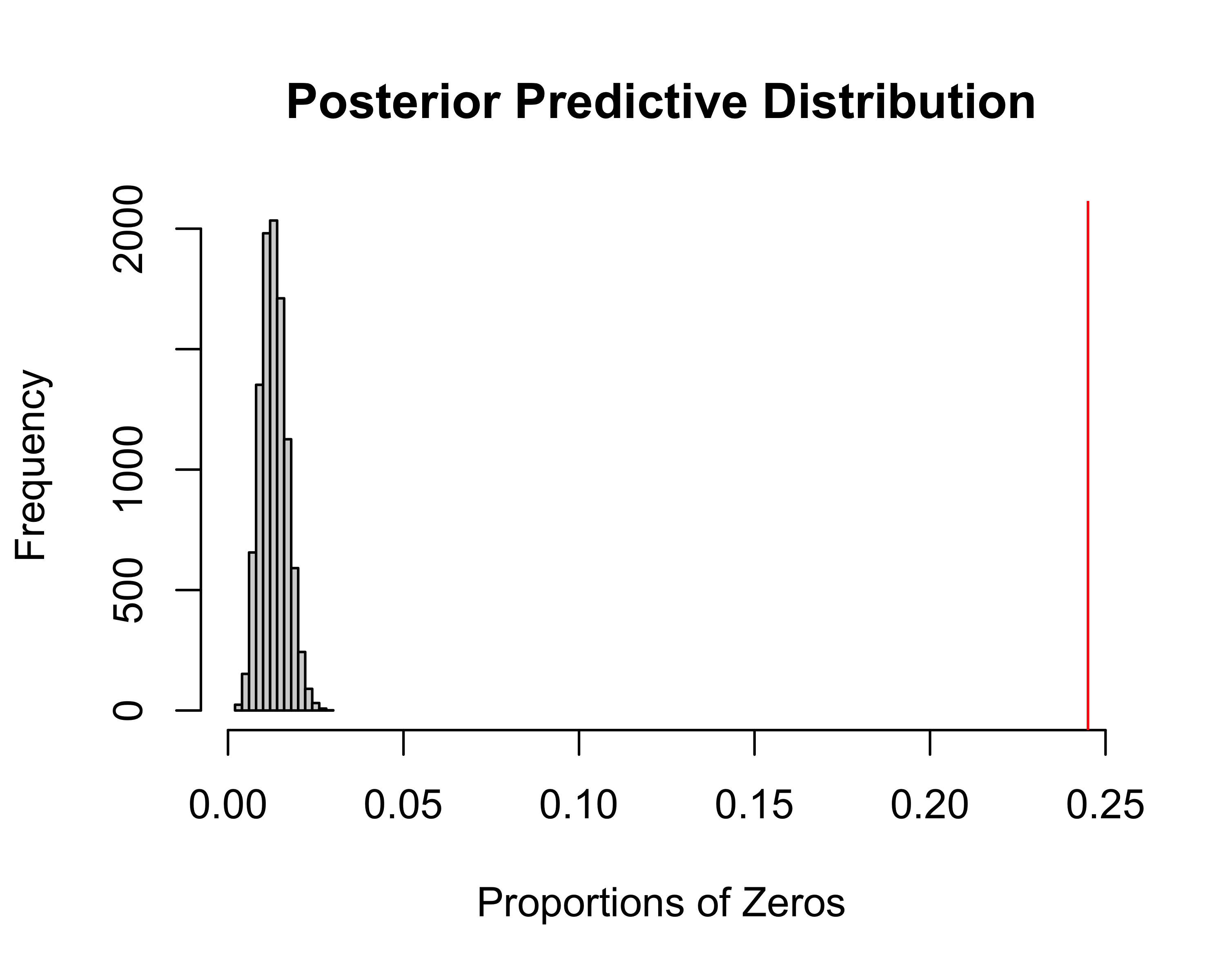
Posterior Predictive p-values (PPPs)

• p-value is probability of seeing something as extreme or more so under a hypothetical “null” model

• from a frequentist perspect, one appealing property of p-values is that they should be uniformally distributed under the “null” model

• PPPs advocated by Gelman & Rubin in papers and BDA are not valid p-values generally. They are do not have a uniform distribution under the hypothesis that the model is correctly specified

• the PPPs tend to be concentrated around 0.5, tend not to reject (conservative)

• theoretical reason for the incorrect distribution is due to double use of the data

• DO NOT USE as a formal test! use as a diagnostic plot to see how model might fall flat, but be cautious!

Example: Bivariate Normal

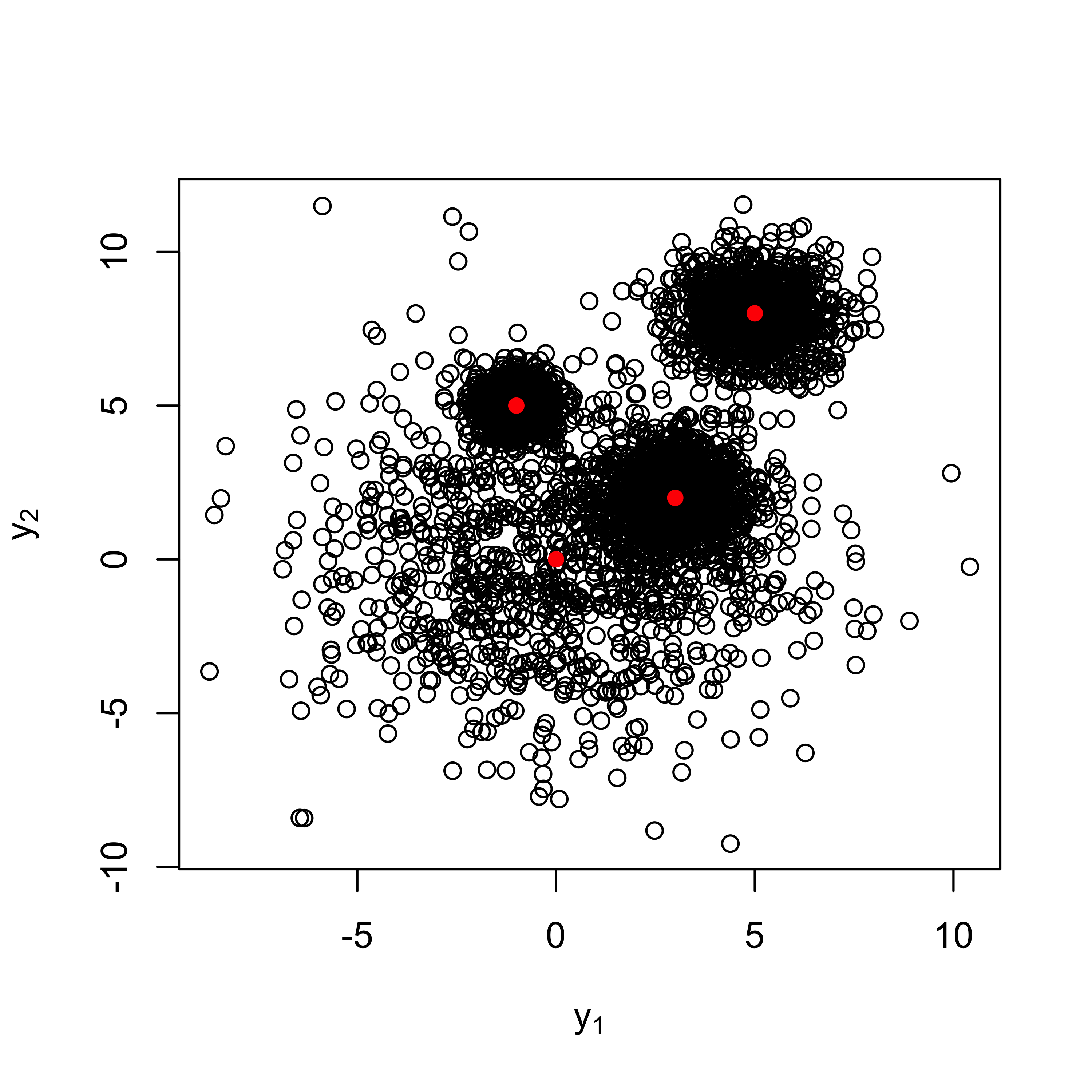
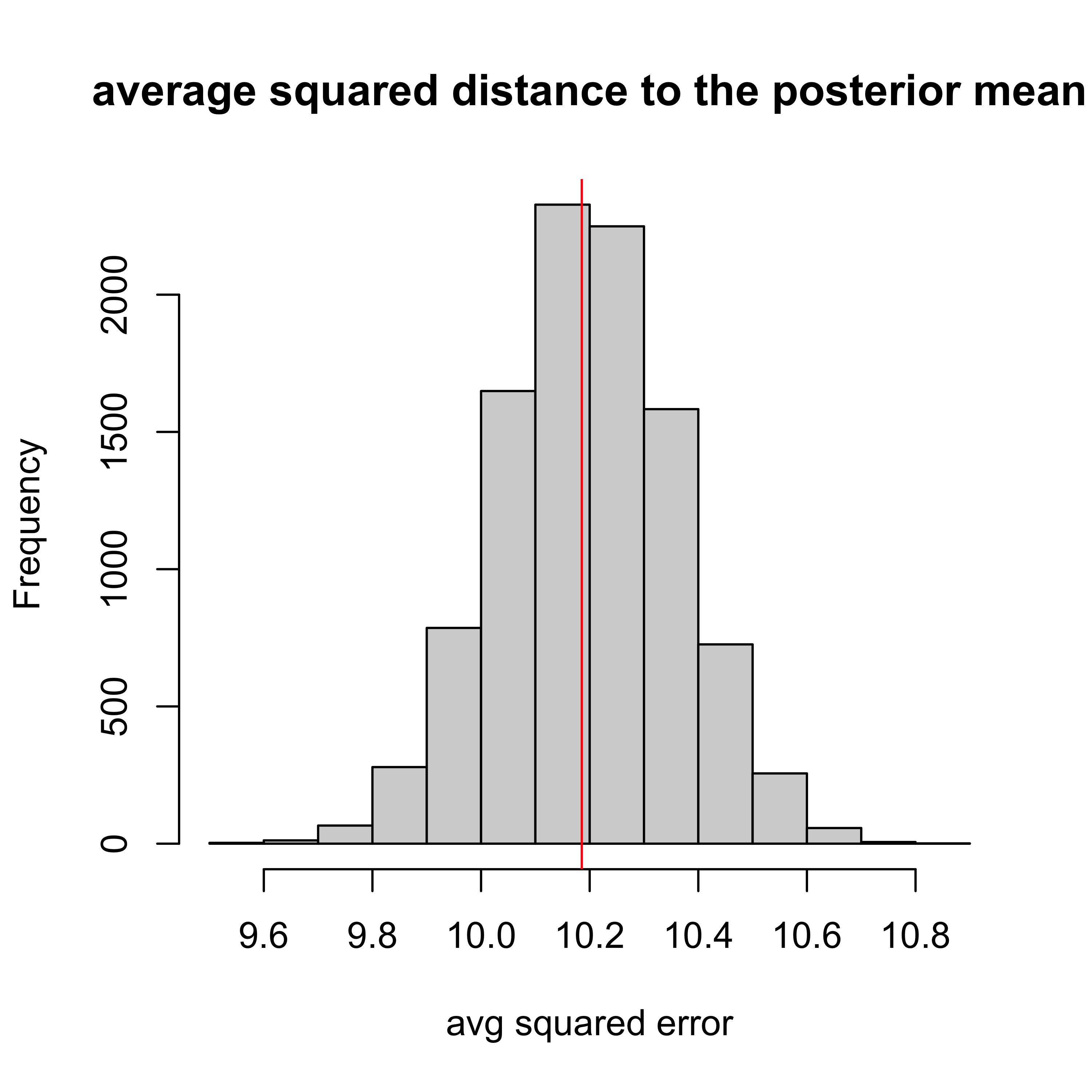
• PPP = 0.52

• What’s happening?

Problems with PPC

• Bayarri & Berger (2000) provides more discussion about why PPP are not always calibrated

• Double use of the data; \(Y^{\text{rep}}\) depends on the observed diagnostic in last case

• Bayarri & Berger propose partial predictive p-values and conditional predictive p-values that avoid double use of the data by “removing” the contribution of \(d_{\text{obs}}\) to the posterior for \(\theta\) or conditioning on a statistic, such as the MLE of \(\theta\)

• heuristically, need the diagnostic to be independent of posterior for \(\theta\) (asymptoptically) under the assumed model

• not always easy to find!

• Moran et al (2022) propose a workaround to avoid double use of the data by spliting the data \(y_{\text{obs}}, y_{\text{new}}\), use \(y_{\text{obs}}\), to learn \(\theta\) and the other to calculate \(d_{\textrm{new}}\)

• can be calculated via simulation easily

POP-PC of Moran et al

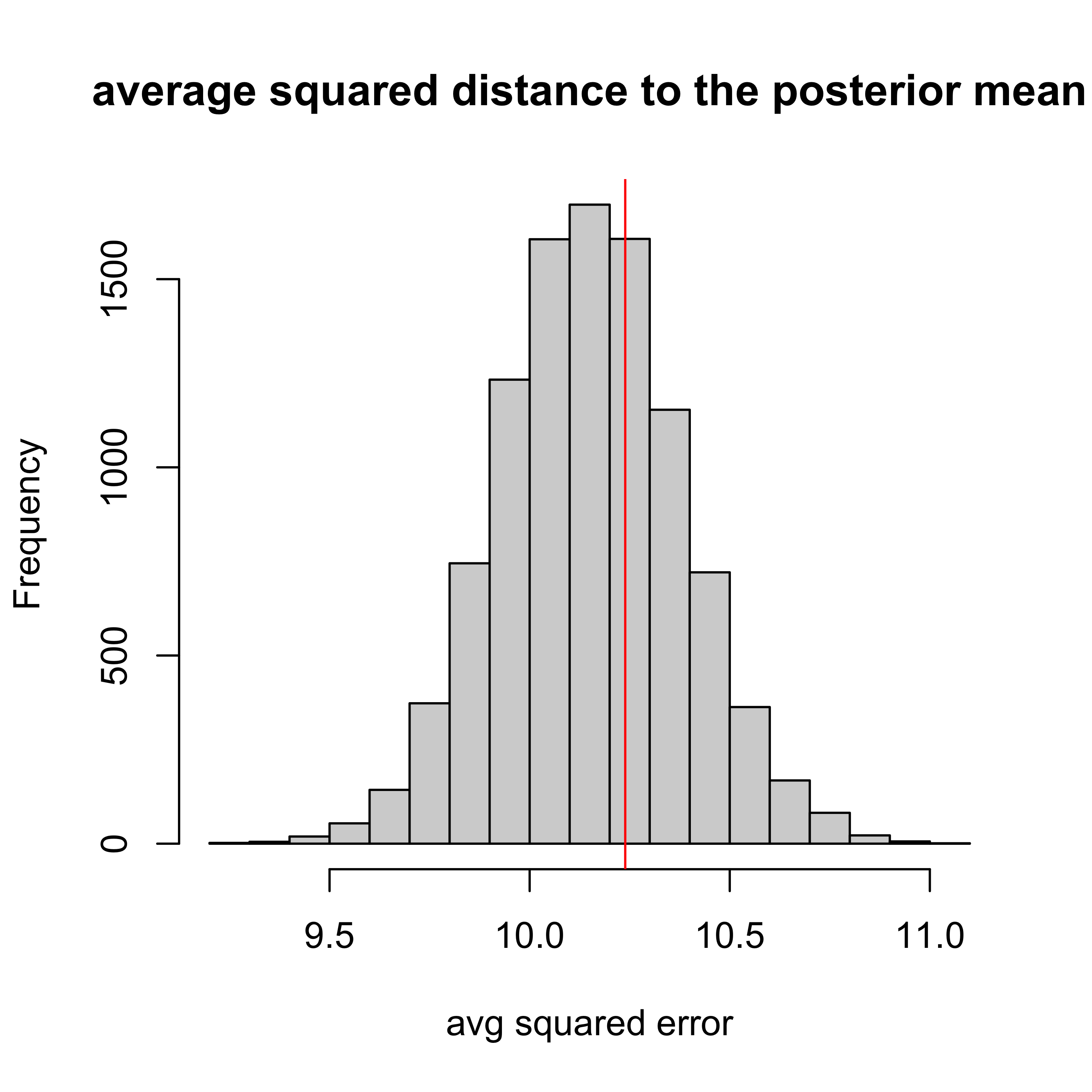
• POP-PPC = 0.35

Modeling Over-Dispersion

• Original Model \(Y_i \mid \theta \sim \textsf{Poisson}(\theta)\)

• cause of overdispersion is variation in the rate \[ Y_i \mid \theta_i \sim \textsf{Poisson}(\theta_i)\]

• model variation via prior \[\theta_i \sim \pi_\theta()\]

• \(\pi_\theta()\) characterizes variation in the rate parameter across inviduals

• Simple Two Stage Hierarchical Model

Modeling Perspectives

1. start with a simple model

• ask if there are surprises through Posterior Checks
• need calibrated diagnostic(s) with good power
• need these to work even if starting model is relatively complex
• other informal diagnostics (residuals)
• remodel if needed based on departures
• Bayesian meaning?

2. start with a fairly complex model or models

• shrinkage to prevent overfitting
• formal tests for simplifying models
• methods to combine multiple models to express uncertaity
• properties

Example

\[\theta_i \sim \textsf{Gamma}(\phi \mu, \phi)\]

• Find pmf for \(Y_i \mid \mu, \phi\)

• Find \(\textsf{E}[Y_i \mid \mu, \phi]\) and \(\textsf{Var}[Y_i \mid \mu, \phi]\)

• Homework: \[\theta_i \sim \textsf{Gamma}(\phi, \phi/\mu)\]

• Can either of these model zero-inflation?